Why I Don't Buy Clustering Axioms

In NIPS 15, Jon Kleinberg presented some impossibility results for clustering. The idea is to specify three axioms that all clustering functions should obey and examine those axioms.

Let (X,d) be a metric space (so X is a discrete set of points and d is a metric over the points of X). A clustering function F takes d as input and produces a clustering of the data. The three axioms Jon states that all clustering functions should satisfy are:

1. Scale invariance: For all d, for all a>0, F(ad) = F(d). In other words, if I transform all my distances by scaling them uniformly, then the output of my clustering function should stay the same.
2. Richness: The range of F is the set of all partitions. In other words, there isn't any bias that prohibits us from producing some particular partition.
3. Consistency: Suppose F(d) gives some clustering, C. Now, modify d by shrinking distances within clusters of C and expanding distances between clusters in C. Call the new metric d'. Then F(d') = C.

Kleinberg's result is that there is no function F that simultaneously satisfies all these requirements. Functions can satisfy two, but never all three. There have been a bunch of follow on papers, including one at NIPS last year and one that I just saw at UAI.

If you think about these axioms a little bit, they kind of make sense. My problem is that if you think about them a lot of bit, you (or at least I) realize that they're broken. The biggest broken one is consistency, which becomes even more broken when combined with scale invariance.

What I'm going to do to convince you that consistency is broken is start with some data in which there is (what I consider) a natural clustering into two clusters. I'll then apply consistency a few times to get something that (I think) should yield a different clustering.

Let's start with some data. The colors are my opinion as to how the data should be clustered:

I hope you agree with my color coding. Now, let's apply consistency. In particular, let's move some of the red points, only reducing inter-clustering distances. Formally, we find the closest pair of points and move things toward those.

The arrows denote the directions these points will be moved. To make the situation more visually appealing, let's move things into lines: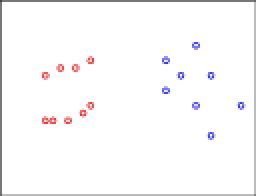
Okay, this is already looking funky. Let's make it even worse. Let's apply consistency again and start moving some blue points:
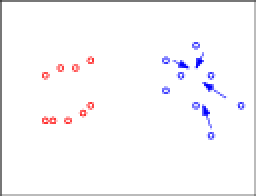Again, let's organize these into a line:
And if I had given you this data to start with, my guess is the clustering you'd have come up with is more like:
This is a violation of consistency.

So, what I'd like someone to do is to argue to my why consistency is actually a desirable property.

I can come up with lots of other examples. One reason why this invariance is bad is because it renders the notion of "reference sizes" irrelevant. This is of course a problem if you have prior knowledge (eg., one thing measured in millimeters, the other in kilometers). But even in the case where you don't know knowledge, what you can do is take the following. Take data generated by thousands of well separated Gaussians, so that the clearly right thing to do is have one cluster per Gaussian. Now, for each of these clusters except for one, shrink them down to single points. This is possible by consistency. Now, your data basically looks like thousands-1 of clusters with zero inter-cluster distances and then one cluster that's spread out. But now it seems that the reasonable thing is to put each data point that was in this old cluster into its own cluster, essentially because I feel like the other data shows you what clusters should look like. If you're not happy with this, apply scaling and push these points out super far from each other. (I don't think this example is as compelling as the one I drew in pictures, but I still think it's reasonable.

Now, in the UAI paper this year, they show that if you fix the number of clusters, these axioms are now consistent. (Perhaps this has to do with the fact that all of my "weird" examples change the number of clusters -- though frankly I don't think this is necessary... I probably could have arranged it so that the resulting green and blue clusters look like a single line that maybe should just be one cluster by itself.) But I still feel like consistency isn't even something we want.

(Thanks to the algorithms group at Utah for discussions related to some of these issues.)

UPDATE 20 JUNE 2009, 3:49PM EST

Here's some data to justify the "bad things happen even when the number of clusters stays the same" claim.

Start with this data:


Now, move some points toward the middle (note they have to spread to the side a bit so as not to decrease intra-cluster distances).

Yielding data like the following:

Now, I feel like two horizontal clusters are most natural here. But you may disagree. What if I add some more data (ie., this is data that would have been in the original data set too, where it clearly would have been a third cluster):

And if you still disagree, well then I guess that's fine. But what if there were hundreds of other clusters like that.

I guess the thing that bugs me is that I seem to like clusters that have similar structures. Even if some of these bars were rotated arbitrarily (or, preferably, in an axis-aligned manner), I would still feel like there's some information getting shared across the clusters.