Some random NIPS thoughts...

I missed the first two days of NIPS due to teaching. Which is sad -- I heard there were great things on the first day. I did end up seeing a lot that was nice. But since I missed stuff, I'll instead post some paper suggests from one of my students, Piyush Rai, who was there. You can tell his biases from his selections, but that's life :). More of my thoughts after his notes...

Says Piyush:

There was an interesting tutorial by Gunnar Martinsson on using randomization to speed-up matrix factorization (SVD, PCA etc) of really really large matrices (by "large", I mean something like 106 x 106). People typically use Krylov subspace methods (e.g., the Lanczos algo) but these require multiple passes over the data. It turns out that with the randomized approach, you can do it in a single pass or a small number of passes (so it can be useful in a streaming setting). The idea is quite simple. Let's assume you want the top K evals/evecs of a large matrix A. The randomized method draws K *random* vectors from a Gaussian and uses them in some way (details here) to get a "smaller version" of A on which doing SVD can be very cheap. Having got the evals/evecs of B, a simple transformation will give you the same for the original matrix A.
The success of many matrix factorization methods (e.g., the Lanczos) also depends on how quickly the spectrum decays (eigenvalues) and they also suggest ways of dealing with cases where the spectrum doesn't quite decay that rapidly.

Some papers from the main conference that I found interesting:

Distribution Matching for Transduction (Alex Smola and 2 other guys): They use maximum mean discrepancy (MMD) to do predictions in a transduction setting (i.e., when you also have the test data at training time). The idea is to use the fact that we expect the output functions f(X) and f(X') to be the same or close to each other (X are training and X' are test inputs). So instead of using the standard regularized objective used in the inductive setting, they use the distribution discrepancy (measured by say D) of f(X) and f(X') as a regularizer. D actually decomposes over pairs of training and test examples so one can use a stochastic approximation of D (D_i for the i-th pair of training and test inputs) and do something like an SGD.

Semi-supervised Learning using Sparse Eigenfunction Bases (Sinha and Belkin from Ohio): This paper uses the cluster assumption of semi-supervised learning. They use unlabeled data to construct a set of basis functions and then use labeled data in the LASSO framework to select a sparse combination of basis functions to learn the final classifier.

Streaming k-means approximation (Nir Ailon et al.): This paper does an online optimization of the k-means objective function. The algo is based on the previously proposed kmeans++ algorithm.

The Wisdom of Crowds in the Recollection of Order Information. It's about aggregating rank information from various individuals to reconstruct the global ordering.

Dirichlet-Bernoulli Alignment: A Generative Model for Multi-Class Multi-Label Multi-Instance Corpora (by some folks at gatech): The problem setting is interesting here. Here the "multi-instance" is a bit of a misnomer. It means that each example in turn can consists of several sub-examples (which they call instances). E.g., a document consists of several paragraphs, or a webpage consists of text, images, videos.

Construction of Nonparametric Bayesian Models from Parametric Bayes Equations (Peter Orbanz): If you care about Bayesian nonparametrics. :) It basically builds on the Kolmogorov consistency theorem to formalize and sort of gives a recipe for the construction of nonparametric Bayesian models from their parametric counterparts. Seemed to be a good step in the right direction.

Indian Buffet Processes with Power-law Behavior (YWT and Dilan Gorur): This paper actually does the exact opposite of what I had thought of doing for IBP. The IBP (akin to the sense of the Dirichlet process) encourages the "rich-gets-richer" phenomena in the sense that a dish that has been already selected by a lot of customers is highly likely to be selected by future customers as well. This leads to the expected number of dishes (and thus the latent-features) to be something like O(alpha* log n). This paper tries to be even more aggressive and makes the relationship have a power-law behavior. What I wanted to do was a reverse behavior -- maybe more like a "socialist IBP" :) where the customers in IBP are sort of evenly distributed across the dishes.

The rest of this post are random thoughts that occurred to me at NIPS. Maybe some of them will get other people's wheels turning? This was originally an email I sent to my students, but I figured I might as well post it for the world. But forgive the lack of capitalization :):

persi diaconis' invited talk about reinforcing random walks... that is, you take a random walk, but every time you cross an edge, you increase the probability that you re-cross that edge (see coppersmith + diaconis, rolles + diaconis).... this relates to a post i had a while ago: nlpers.blogspot.com/2007/04/multinomial-on-graph.html ... i'm thinking that you could set up a reinforcing random walk on a graph to achieve this. the key problem is how to compute things -- basically want you want is to know for two nodes i,j in a graph and some n >= 0, whether there exists a walk from i to j that takes exactly n steps. seems like you could craft a clever data structure to answer this question, then set up a graph multinomial based on this, with reinforcement (the reinforcement basically looks like the additive counts you get from normal multinomials)... if you force n=1 and have a fully connected graph, you should recover a multinomial/dirichlet pair.

also from persi's talk, persi and some guy sergei (sergey?) have a paper on variable length markov chains that might be interesting to look at, perhaps related to frank wood's sequence memoizer paper from icml last year.

finally, also from persi's talk, steve mc_something from ohio has a paper on using common gamma distributions in different rows to set dependencies among markov chains... this is related to something i was thinking about a while ago where you want to set up transition matrices with stick-breaking processes, and to have a common, global, set of sticks that you draw from... looks like this steve mc_something guy has already done this (or something like it).

not sure what made me think of this, but related to a talk we had here a few weeks ago about unit tests in scheme, where they basically randomly sample programs to "hope" to find bugs... what about setting this up as an RL problem where your reward is high if you're able to find a bug with a "simple" program... something like 0 if you don't find a bug, or 1/|P| if you find a bug with program P. (i think this came up when i was talking to percy -- liang, the other one -- about some semantics stuff he's been looking at.) afaik, no one in PL land has tried ANYTHING remotely like this... it's a little tricky because of the infinite but discrete state space (of programs), but something like an NN-backed Q-learning might do something reasonable :P.

i also saw a very cool "survey of vision" talk by bill freeman... one of the big problems they talked about was that no one has a good p(image) prior model. the example given was that you usually have de-noising models like p(image)*p(noisy image|image) and you can weight p(image) by ^alpha... as alpha goes to zero, you should just get a copy of your noisy image... as alpha goes to infinity, you should end up getting a good image, maybe not the one you *want*, but an image nonetheless. this doesn't happen.

one way you can see that this doesn't happen is in the following task. take two images and overlay them. now try to separate the two. you *clearly* need a good prior p(image) to do this, since you've lost half your information.

i was thinking about what this would look like in language land. one option would be to take two sentences and randomly interleave their words, and try to separate them out. i actually think that we could solve this tasks pretty well. you could probably formulate it as a FST problem, backed by a big n-gram language model. alternatively, you could take two DOCUMENTS and randomly interleave their sentences, and try to separate them out. i think we would fail MISERABLY on this task, since it requires actually knowing what discourse structure looks like. a sentence n-gram model wouldn't work, i don't think. (although maybe it would? who knows.) anyway, i thought it was an interesting thought experiment. i'm trying to think if this is actually a real world problem... it reminds me a bit of a paper a year or so ago where they try to do something similar on IRC logs, where you try to track who is speaking when... you could also do something similar on movie transcripts.

hierarchical topic models with latent hierarchies drawn from the coalescent, kind of like hdp, but not quite. (yeah yeah i know i'm like a parrot with the coalescent, but it's pretty freaking awesome :P.)


That's it! Hope you all had a great holiday season, and enjoy your New Years (I know I'm going skiing. A lot. So there, Fernando! :)).

From Kivenen/Warmuth and EG to CW learning and Adaptive Regularization

This post is a bit of a historical retrospective, because it's only been recently that these things have aligned themselves in my head.

The all goes back to Jyrki Kivenen and Manfred Warmuth's paper on exponentiated gradient descent that dates back to STOC 1995. For those who haven't read this paper, or haven't read it recently, it's a great read (although it tends to repeat itself a lot). It's particularly interesting because they derive gradient descent and exponentiated gradient descent (GD and EG) as a consequence of other assumptions.

In particular, suppose we have an online learning problem, where at each time step we receive an example x, make a linear prediction (w'x) and then suffer a loss. The idea is that if we suffer no loss, then we leave w as is; if we do suffer a loss, then we want to balance two goals:

1. Change w enough so that we wouldn't make this error again
2. Don't change w too much

The key question is how to define "too much." Suppose that we measure changes in w by looking at Euclidean distance between the updated w and the old w. If we work through the math for enforcing 1 while minimizing 2, we derive the gradient descent update rule that's been used for optimizing, eg., perceptrons for squared loss for ages.

The magic is what happens if we use something other than Euclidean distance. If, instead, we assume that the ws are all positive, we can use an (unnormalized) KL divergence to measure differences between weight vectors. Doing this leads to multiplicative updates, or the exponentiated gradient algorithm.

(Obvious (maybe?) open question: what happens if you replace the distance with some other divergence, say a Bregman, or alpha or phi-divergence?)

This line of thinking leads naturally to Crammer et al.'s work on Online Passive Aggressive algorithms, from JMLR 2006. Here, the idea remains the same, but instead of simply ensuring that we make a correct classification, ala rule (1) above, we ensure that we make a correct classification with a margin of at least 1. They use Euclidean distance to measure the difference in weight vectors, and, for many cases, can get closed-form updates that look GD-like, but not exactly GD. (Aside: what happens if you use, eg., KL instead of Euclidean?)

Two years later, Mark Dredze, Koby Crammer and Fernando Pereira presented Confidence-Weighted Linear Classification. The idea here is the same: don't change the weight vectors too much, but achieve good classification. The insight here is to represent weight vectors by distributions over weight vectors, and the goal is to change these distributions enough, but not too much. Here, we go back to KL, because KL makes more sense for distributions, and make a Gaussian assumption on the weight vector distribution. (This has close connections both to PAC-Bayes and, if I'm wearing my Bayesian hat, Kalman filtering when you make a Gaussian assumption on the posterior, even though it's not really Gaussian... it would be interesting to see how these similarities play out.)

The cool thing here is that you effectively get variable learning rates on different parameters, where confident parameters get moved less. (In practice, one really awesome effect is that you tend to only need one pass over your training data to do a good job!) If you're interested in the Bayesian connection, you can get a very similar style algorithm if you do EP on a Bayesian classification algorithm (by Stern, Herbrich and Graepel), which is what Microsoft Bing uses for online ads.

This finally bring us to NIPS this year, where Koby Crammer, Alex Kulesza and Mark Dredze presented work on Adaptive Regularization of Weight Vectors. Here, they take Confidence Weighted classification and turn the constraints into pieces of the regularizer (somewhat akin to doing a Lagrangian trick). Doing so allows them to derive a representer theorem. But again, the intuition is exactly the same: don't change the classifier too much, but enough.

All in all, this is a very interesting line of work. The reason I'm posting about it is because I think seeing the connections makes it easier to sort these different ideas into bins in my head, depending on what your loss is (squared versus hinge), what your classifier looks like (linear versus distribution over linear) and what your notion of "similar classifiers" is (Euclidean or KL).

(Aside: Tong Zhang has a paper on regularized winnow methods, which fits in here somewhere, but not quite as cleanly.)

K-means vs GMM, sum-product vs max-product

I finished K-means and Gaussian mixture models in class last week or maybe the week before. I've previously discussed the fact that these two are really solving different problems (despite being structurally so similar), but today's post is about something different.

There are two primary differences between the typical presentation of K-means and the typical presentation of GMMs. (I say "typical" because you can modify these algorithms fairly extensively as you see fit.) The first difference is that GMMs just have more parameters. The parameters of K-means are typically the cluster assignments ("z") and the means ("mu"). The parameters of a GMM are typically these (z and mu) as well as the class prior probabilities ("pi") and cluster covariances ("Sigma"). The GMM model is just richer. Of course, you can restrict it so all clusters are isotropic and all prior probabilities are even, in which case you've effectively removed this difference (or you can add these things into K-means). The second difference is that GMMs operate under the regime of "soft assignments," meaning that points aren't wed to clusters: they only prefer (in a probabilistic sense) some clusters to others. This falls out naturally from the EM formalization, where the soft assignments are simply the expectations of the assignments under the current model.

One can get rid of the second difference by running "hard EM" (also called "Viterbi EM" in NLP land), where the expectations are clamped at their most likely value. This leads to something that has much more of a K-means feel.

This "real EM" versus "hard EM" distinction comes up a lot in NLP, where computing exact expectations is often really difficult. (Sometimes you get complex variants, like the "pegging" approaches in the IBM machine translation models, but my understanding from people who run in this circle is that pegging is much ado about nothing.) My general feeling has always been "if you don't have much data, do real EM; if you have tons of data, hard EM is probably okay." (This is purely from a practical perspective.) The idea is that when you have tons and tons of data, you can approximate expectations reasonably well by averaging over many data points. (Yes, this is hand-wavy and it's easy to construct examples where it fails. But it seems to work many times.) Of course, you can get pedantic and say "hard EM sucks: it's maximizing p(x,z) but I really want to maximize p(x)" to which I say: ho hum, who cares, you don't actually care about p(x), you care about some extrinsic evaluation metric which, crossing your fingers, you hope correlates with p(x), but for all I know it correlates better with p(x,z).

Nevertheless, a particular trusted friend has told me he's always remiss when he can't do full EM and has to do hard EM: he's never seen a case where it doesn't help. (Or maybe "rarely" would be more fair.) Of course, this comes at a price: for many models, maximization (search) can be done in polynomial time, but computing expectations can be #P-hard (basically because you have to enumerate -- or count -- over every possible assignment).

Now let's think about approximate inference in graphical models. Let's say I have a graphical model with some nodes I want to maximize over (call them "X") and some nodes I want to marginalize out (call them "Z"). For instance, in GMMs, the X nodes would be the means, covariances and cluster priors; the Z nodes would be the assignments. (Note that this is departing slightly from typical notation for EM.) Suppose I want to do inference in such a model. Here are three things I can do:

1. Just run max-product. That is, maximize p(X,Z) rather than p(X).
2. Just run sum-product. That is, compute expectations over X and Z, rather than just over Z.
3. Run EM, by alternating something like sum-product on Z and something like max-product onX.

Of these, only (3) is really doing the "right thing." Further, let's get away from the notion of p(X) not correlating with some extrinsic evaluation by just measuring ourselves against exact inference. (Yes, this limits us to relatively small models with 10 or 20 binary nodes.)

What do you think happens? Well, first, things vary as a function of the number of X nodes versus Z nodes in the graph.

When most of the nodes are X (maximization) nodes, then max-product does best and EM basically does the same.

Whe most of the nodes are Z (marginalization) nodes, then EM does best and sum-product does almost the same. But max product also does almost the same.

This is an effect that we've been seeing regularly, regardless of what the models look like (chains or lattices), what the potentials look like (high temperature or low temperature) and how you initialize these models (eg., in the chain case, EM converges to different places depending on initialization, while sum- and max-product do not). Max product is just unbeatable.

In a sense, from a practical perspective, this is nice. It says: if you have a mixed model, just run max product and you'll do just as well as if you had done something more complicated (like EM). But it's also frustrating: we should be getting some leverage out of marginalizing over the nodes that we should marginalize over. Especially in the high temperature case, where there is lots of uncertainty in the model, max product should start doing worse and worse (note that when we evaluate, we only measure performance on the "X" nodes -- the "Z" nodes are ignored).

Likening this back to K-means versus GMM, for the case where the models are the same (GMM restricted to not have priors or covariances), the analogy is that as far as the means go, it doesn't matter which one you use. Even if there's lots of uncertainty in the data. Of course, you may get much better assignments from GMM (or you may not, I don't really know). But if all you really care about at the end of the day are the Xs (the means), then our experience with max-product suggests that it just won't matter. At all. Ever.

Part of me finds this hard to believe, and note that I haven't actually run experiments with K-means and GMM, but the results in the graphical model cases are sufficiently strong and reproducible that I'm beginning to trust them. Shouldn't someone have noticed this before, though? For all the effort that's gone into various inference algorithms for graphical models, why haven't we ever noticed that you just can't beat max-product?

(Yes, I'm aware of some theoretical results, eg., the Wainwright result that sum-product + randomized rounding is a provably good approximation to the MAP assignment, but this result actually goes the other way, and contradicts many of our experimental studies where sum-product + rounding just flat out sucks. Maybe there are other results out there that we just haven't been able to dig up.)

NLP as a study of representations

Ellen Riloff and I run an NLP reading group pretty much every semester. Last semester we covered "old school NLP." We independently came up with lists of what we consider some of the most important ideas (idea = paper) from pre-1990 (most are much earlier) and let students select which to present. There was a lot of overlap between Ellen's list and mine (not surprisingly). If people are interested, I can provide the whole list (just post a comment and I'll dig it up). The whole list of topics is posted as a comment. The topics that were actually selected are here.

I hope the students have found this exercise useful. It gets you thinking about language in a way that papers from the 2000s typically do not. It brings up a bunch of issues that we no longer think about frequently. Like language. (Joking.) (Sort of.)

One thing that's really stuck out for me is how much "old school" NLP comes across essentially as a study of representations. Perhaps this is a result of the fact that AI -- as a field -- was (and, to some degree, still is) enamored with knowledge representation problems. To be more concrete, let's look at a few examples. It's already been a while since I read these last (I had meant to write this post during the spring when things were fresh in my head), so please forgive me if I goof a few things up.

I'll start with one I know well: Mann and Thompson's rhetorical structure theory paper from 1988. This is basically "the" RST paper. I think that when a many people think of RST, they think of it as a list of ways that sentences can be organized into hierarchies. Eg., this sentence provides background for that one, and together they argue in favor of yet a third. But this isn't really where RST begins. It begins by trying to understand the communicative role of text structure. That is, when I write, I am trying to communicate something. Everything that I write (if I'm writing "well") is toward that end. For instance, in this post, I'm trying to communicate that old school NLP views representation as the heart of the issue. This current paragraph is supporting that claim by providing a concrete example, which I am using to try to convince you of my claim.

As a more detailed example, take the "Evidence" relation from RST. M+T have the following characterization of "Evidence." Herein, "N" is the nucleus of the relation, "S" is the satellite (think of these as sentences), "R" is the reader and "W" is the writer:

relation name: Evidence
constraints on N: R might not believe N to a degree satisfactory to W
constraints on S: R believes S or will find it credible
constraints on N+S: R's comprehending S increases R's belief of N
the effect: R's belief of N is increased
locus of effect: N

This is a totally different way from thinking about things than I think we see nowadays. I kind of liken it to how I tell students not to program. If you're implementing something moderately complex (say, forward/backward algorithm), first write down all the math, then start implementing. Don't start implementing first. I think nowadays (and sure, I'm guilty!) we see a lot of implementing without the math. Or rather, with plenty of math, but without a representational model of what it is that we're studying.

The central claim of the RST paper is that one can think of texts as being organized into elementary discourse units, and these are connected into a tree structure by relations like the one above. (Or at least this is my reading of it.) That is, they have laid out a representation of text and claimed that this is how texts get put together.

As a second example (this will be sorter), take Wendy Lehnert's 1982 paper, "Plot units and narrative summarization." Here, the story is about how stories get put together. The most interesting thing about the plot units model to me is that it breaks from how one might naturally think about stories. That is, I would naively think of a story as a series of events. The claim that Lehnert makes is that this is not the right way to think about it. Rather, we should think about stories as sequences of affect states. Effectively, an affect state is how a character is feeling at any time. (This isn't quite right, but it's close enough.) For example, Lehnert presents the following story:

When John tried to start his care this morning, it wouldn't turn over. He asked his neighbor Paul for help. Paul did something to the carburetor and got it going. John thanked Paul and drove to work.

The representation put forward for this story is something like: (1) negative-for-John (the car won't start), which leads to (2) motivation-for-John (to get it started, which leads to (3) positive-for-John (it's started), when then links back and resolves (1). You can also analyze the story from Paul's perspective, and then add links that go between the two characters showing how things interact. The rest of the paper describes how these relations work, and how they can be put together into more complex event sequences (such as "promised request bungled"). Again, a high level representation of how stories work from the perspective of the characters.

So now I, W, hope that you, R, have an increased belief in the title of the post.

Why do I think this is interesting? Because at this point, we know a lot about how to deal with structure in language. From a machine learning perspective, if you give me a structure and some data (and some features!), I will learn something. It can even be unsupervised if it makes you feel better. So in a sense, I think we're getting to a point where we can go back, look at some really hard problems, use the deep linguistic insights from two decades (or more) ago, and start taking a crack at things that are really deep. Of course, features are a big problem; as a very wise man once said to me: "Language is hard. The fact that statistical association mining at the word level made it appear easy for the past decade doesn't alter the basic truth. :-)." We've got many of the ingredients to start making progress, but it's not going to be easy!

Getting Started In: Bayesian NLP

This isn't so much a post in the "GSI" series, but just two links that recently came out. Kevin Knight and Philip Resnik both just came out with tutorials for Bayesian NLP. They're both excellent, and almost entirely non-redundant. I highly recommend reading both. And I thank Kevin and Philip from the bottom of my heart, since I'd been toying with the idea of writing such a thing (for a few years!) and they've saved me the effort. I'd probably start with Kevin's and then move on to Philip's (which is more technically meaty), but either order is really fine.

• Bayesian Inference with Tears by Kevin
• Gibbs Sampling for the Uninitiated by Philip

Thanks again to both of them. (And if you haven't read Kevin's previous workbook on SMT -- which promises free beer! -- I highly recommend that, too.)

Convex or not, my schizophrenic personality

Machine learning as a field has been very convex-happy for the past decade or so. So much so that when I saw a tutorial on submodular optimization in ML (one of the best tutorials I've seen), they said something along the lines of "submodularity will be for this decade what convexity was for the last decade." (Submodularity is cool and I'll post about it more in the future, but it's kind of a discrete analog of convexity. There's a NIPS workshop on the topic coming up.) This gives a sense of how important convexity has been.

There's also a bit of an undercurrent of "convexity isn't so great" from other sides of the ML community (roughly from the neural nets folks); see, for instance, Yann LeCun's talk Who's Afraid of Non-convex Loss Functions, a great and entertaining talk.

There's a part of me that loves convexity. Not having to do random restarts, being assured of global convergence, etc., all sounds very nice. I use logistic regression/maxent for almost all of my classification needs, have never run a neural network, and have only occasionally used svms (though of course they are convex, too). When I teach ML (as I'm doing now), I make a bit deal about convexity: it makes life easy in many ways.

That said, almost none of my recent papers reflect this. In fact, in the structure compilation paper, we flat out say that non-linearity in the model (which leads to a non-convex loss function) is the major reason why CRFs outperform independent classifiers in structured prediction tasks! Moreover, whenever I start doing Bayesian stuff, usually solved with some form of MCMC, I've completely punted on everything convex. In a "voting with my feet" world, I could care less about convexity! For the most part, if you're using EM or sampling or whatever, you don't care much about it either. Somehow we (fairly easily!) tolerate whatever negative effects there are of non-convex optimization.

I think one reason why such things don't both us, as NLPers, as much as they bother the average machine learning person is that we are willing to invest some energy in intelligent initialization. This already puts us in a good part of the optimization landscape, and doing local hillclimbing from there is not such a big deal. A classic example is the "Klein and Manning" smart initializer for unsupervised parsing, where a small amount of human knowledge goes a long way above a random initializer.

Another style of initialization is the IBM alignment model style. IBM model 4 is, of course, highly non-convex and ridiculously difficult to optimize (the E step is intractable). So they do a smart initialization, using the output of model 3. Model 3, too, is highly non-convex (but not quite so much so), so they initialize with model 2. And so on, down to model 1, which is actually convex and fairly easy to optimize. This sequencing of simple models to complex models also happens in some statistical analysis, where you first fit first order effects and then later fit higher order effects. The danger, of course, is that you got to a bad hill to climb, but this overall generally appears to be a bigger win than starting somewhere in the middle of a random swamp. (Of course, later, Bob Moore had this cute argument that even though model 1 is convex, we don't actually ever optimize it to the global optimum, so doing clever initialization for model 1 is also a good idea!)

These two ideas: clever initialization, and sequential initialization, seem like powerful ideas that I would like to see make their way into more complex models. For instance, in the original LDA paper, Dave Blei used an initialization where they pick some random documents as seeds for topics. As far as I know, no one really does this anymore (does anyone know why: does it really not matter?), but as we keep building more and more complex models, and lose hope that our off the shelf optimizer (or sampler) is going to do anything reasonable, we're probably going to need to get back to this habit, perhaps trying to formalize it in the meantime.

Some notes on job search

There are tons of "how to apply for academic jobs" write-ups out there; this is not one of them. It's been four years (egads!) since I began my job search and there are lots of things I think I did well and lots of things I wish I had done differently.

When I entered grad school, I was fairly sure that I eventually wanted a university job. During high school, my career goal was to be a high school math teacher. Then I went to college and realized that, no, I wanted to teach math to undergraduates. Then I was an advanced undergraduate and realized that I wanted to teach grads and do research. Teaching was always very important to me, though of course I fell in love with research later. It was unfortunate that it took so long for me to actually get involved in research, but my excuse was that I wasn't in CS, where REU-style positions are plentiful and relatively easy to come by (system development, anyone?).

However, the more time I spend in grad school, including an internship at MSR with Eric Brill (but during which I befriended many in the NLP group at MSR, a group that I still love), I realized that industry labs were a totally great place to go, too.

I ended up applying to basically everything under the sun, provided they had a non-zero number of faculty in either NLP or ML. I talked (mostly off the record) with a few people about post-doc positions (I heard later than simultaneously exploring post-docs and academic positions is not a good idea: hiring committees don't like to "reconsider" people; I don't know how true this is, but I heard it too late myself to make any decisions based on it), applied for some (okay, many) tenure-track positions, some research-track positions (okay, few) and to the big three industry labs. I wrote three cover letters, one more tailored to NLP, one more to ML and one more combined, three research statements (ditto) and one teaching statement. In retrospect, they were pretty reasonable, I think, though not fantastic. I don't think I did enough to make my future research plans not sound like "more of the same."

I suppose my biggest piece of advice for applying is (to the extent possible) find someone you know and trust at the institution and try to figure out exactly what they're looking for. Obviously you can't change who you are and the work you've done, but you definitely can sell it in slightly different ways. This is why I essentially had three application packages -- the material was the same, the focus was different. But, importantly, they were all true. The more this person trusts you, the more of the inside scoop they can give you. For instance, we had a robotics/ML position open (which, sadly, we had to close due to budget issues), but in talking to several ML people, they felt that they weren't sufficiently "robotics" enough; I think I was able to dissuade them of this opinion and we ended up getting a lot of excellent applicants before we shut down the slot.

Related, it's hard to sell yourself across two fields. At the time I graduated, I saw myself as basically straddling NLP and ML. This can be a hard sell to make. I feel in retrospect that you're often better off picking something and really selling that aspect. From the other side of the curtain, what often happens is that you need an advocate (or two) in the department to which you're applying. If you sell yourself as an X person, you can get faculty in X behind you; if you sell yourself as a Y person, you can get faculty in Y behind you. However, if you sell yourself as a mix, the X faculty might prefer a pure X and the Y faculty might prefer a pure Y. Of course, this isn't always true: Maryland is basically looking for a combined NLP/ML person this year to compliment their existing strengths. Of course, this doesn't always hold: this is something that you should try to find out from friends at the places to which you're applying.

For the application process itself, my experience here and what I've heard from most (but not all) universities is that interview decisions (who to call in) get made by a topic-specific hiring committee. This means that to get in the door, you have to appeal to the hiring committee, which is typically people in your area, if it's an area-specific call for applications. Typically your application will go to an admin, first, who will filter based on your cover letter to put you in the right basket (if there are multiple open slots) or the waste basket (for instance, if you don't have a PhD). It then goes to the hiring committee. Again, if you have a friend in the department, it's not a bad idea to let them know by email that you've applied after everything has been submitted (including letters) to make sure that you don't end up in the waste bin.

Once your application gets to the hiring committee, the hope is that they've already heard of you. But if they haven't, hopefully they've heard of at least one of your letter writers. When we get applications, I typically first sort by whether I've heard of the applicant, then by the number of letter writers they have that I've heard of, then loosely by the reputation of their university. And I make my way down the list, not always all the way to the bottom. (Okay, I've only done this once, and I think I got about 90% of the way through.)

In my experience, what we've looked for in applications is (a) a good research statement, including where you're going so as to distinguish yourself from your advisor, (b) a not-bad teaching statement (it's hard to get a job at a research university on a great teaching statement, but it's easy to lose an offer on a bad one... my feeling here is just to be concrete and not to pad it with BS -- if you don't have much to say, don't say much), (c) great letters, and (d) an impressive CV. You should expect that the hiring committee will read some of your papers before interviewing you. This means that if you have dozens, you should highlight somewhere (probably the research statement) what are they best ones that they should read. Otherwise they'll choose essentially randomly, and (depending on your publishing style) this could hurt. As always, put your best foot forward and make it easy for the hiring committee to find out what's so great about you.

Anyway, that's basically it. There's lots more at interview stage, but these are my feelings for application stage. I'd be interested to hear if my characterization of the hiring process is vastly different than at other universities; plus, if there are other openings that might be relevant to NLP/ML folks, I'm sure people would be very pleased to seem them in the comments section.

Good luck, all your graduating folks!

Where did you Apply to Grad School?

Ellen and I are interested (for obvious reasons) in how people choose what schools to apply to for grad school. Note that this is not the question of how you chose where to go. This is about what made the list of where you actually applied. We'd really appreciate if you'd fill out our 10-15 minute survey and pass it along to your friends (and enemies). If you're willing, please go here.

ACL and EMNLP retrospective, many days late

Well, ACL and EMNLP are long gone. And sadly I missed one day of each due either to travel or illness, so most of my comments are limited to Mon/Tue/Fri. C'est la vie. At any rate, here are the papers I saw or read that I really liked.

• P09-1010 [bib]: S.R.K. Branavan; Harr Chen; Luke Zettlemoyer; Regina Barzilay
  Reinforcement Learning for Mapping Instructions to Actions
  
  and
  

  P09-1011 [bib]: Percy Liang; Michael Jordan; Dan Klein
  Learning Semantic Correspondences with Less Supervision
  
  these papers both address what might roughly be called the grounding problem, or at least trying to learn something about semantics by looking at data. I really really like this direction of research, and both of these papers were really interesting. Since I really liked both, and since I think the directions are great, I'll take this opportunity to say what I felt was a bit lacking in each. In the Branavan paper, the particular choice of reward was both clever and a bit of a kludge. I can easily imagine that it wouldn't generalize to other domains: thank goodness those Microsoft UI designers happened to call the Start Button something like UI_STARTBUTTON. In the Liang paper, I worry that it relies too heavily on things like lexical match and other very domain specific properties. They also should have cited Fleischman and Roy, which Branavan et al did, but which many people in this area seem to miss out on -- in fact, I feel like the Liang paper is in many ways a cleaner and more sophisticated version of the Fleischman paper.
  

• P09-1054 [bib]: Yoshimasa Tsuruoka; Jun’ichi Tsujii; Sophia Ananiadou
  Stochastic Gradient Descent Training for L1-regularized Log-linear Models with Cumulative Penalty
  
  This paper is kind of an extension of the truncated gradient approach to learning l1-regularized models that John, Lihong and Tong had last year at NIPS. The paper did a great job at motivated why L1 penalties is hard. The first observation is that L1 regularizes optimized by gradient steps like to "step over zero." This is essentially the observation in truncated gradient and frankly kind of an obvious one (I always thought this is how everyone optimized these models, though of course John, Lihong and Tong actually proved something about it). The second observation, which goes into this current paper, is that you often end up with a lot of non-zeros simply because you haven't run enough gradient steps since the last increase. They have a clever way to accumulating these penalties lazily and applying them at the end. It seems to do very well, is easy to implement, etc. But they can't (or haven't) proved anything about it.

• P09-1057 [bib]: Sujith Ravi; Kevin Knight
  Minimized Models for Unsupervised Part-of-Speech Tagging
  
  I didn't actually see this paper (I think I was chairing a session at the time), but I know about it from talking to Sujith. Anyone who considers themselves a Bayesian in the sense of "let me put a prior on that and it will solve all your ills" should read this paper. Basically they show that sparse priors don't give you things that are sparse enough, and that by doing some ILP stuff to minimize dictionary size, you can get tiny POS tagger models that do very well.
  

• D09-1006: [bib] Omar F. Zaidan; Chris Callison-Burch
  Feasibility of Human-in-the-loop Minimum Error Rate Training
  
  Chris told me about this stuff back in March when I visited JHU and I have to say I was totally intrigued. Adam already discussed this paper in an earlier post, so I won't go into more details, but it's definitely a fun paper.
  
  
• D09-1011: [bib] Markus Dreyer; Jason Eisner
  Graphical Models over Multiple Strings
  
  This paper is just fun from a technological perspective. The idea is to have graphical models, but where nodes are distributions over strings represented as finite state automata. You do message passing, where your messages are now automata and you get to do all your favorite operations (or at least all of Jason's favorite operations) like intersection, composition, etc. to compute beliefs. Very cool results.
  
  
• D09-1024: [bib] Ulf Hermjakob
  Improved Word Alignment with Statistics and Linguistic Heuristics
  
  Like the Haghighi coreference paper below, here we see how to do word alignment without fancy math!
  
  
• D09-1120: [bib] Aria Haghighi; Dan Klein
  Simple Coreference Resolution with Rich Syntactic and Semantic Features
  
  How to do coreference without math! I didn't know you could still get papers accepted if they didn't have equations in them!

In general, here's a trend I've seen in both ACL and EMNLP this year. It's the "I find a new data source and write a paper about it" trend. I don't think this trend is either good or bad: it simply is. A lot of these data sources are essentially Web 2.0 sources, though some are not. Some are Mechanical Turk'd sources. Some are the Penn Discourse Treebank (about which there were a ridiculous number of papers: it's totally unclear to me why everyone all of a sudden thinks discourse is cool just because there's a new data set -- what was wrong with the RST treebank that it turned everyone off from discourse for ten years?! Okay, that's being judgmental and I don't totally feel that way. But I partially feel that way.)

Classifier performance: alternative metrics of success

I really enjoyed Mark Dredze's talk at EMNLP on multiclass confidence weighted algorithms, where they take their CW binary predictors and extend them in two (basically equivalent) ways to a multiclass/structured setting (warning: I haven't read the paper!). Mark did a great job presenting, as always, and dryly suggested that we should all throw away our perceptrons and our MIRAs and SVMs and just switch to CW permanently. It was a pretty compelling case.

Now, I'm going to pick on basically every "yet another classifier" paper I've read in the past ten years (read: ever). I'm not trying to point fingers, but just try to better understand why I, personally, haven't yet switched to using these things and continue to use either logistic regression or averaged perceptron for all of my classification needs (aside from the fact that I am rather fond of a particular software package for doing these things -- note, though, that it does support PA and maybe soon CW if I decide to spend 10 minutes implementing it!).

Here's the deal. Let's look at SVM versus logreg. Whether this is actually true or not, I have this gut feeling that logreg is much less sensitive to hyperparameter selection than are SVMs. This is not at all based on any science, and the experience that it's based on it somewhat unfair (comparing megam to libSVM, for instance, which use very different optimization methods, and libSVM doesn't do early stopping while megam does). However, I've heard from at least two other people that they have the same internal feelings. In other words, here's a caricature of how I believe logreg and SVM behave:



That is, if you really tune the regularizer (lambda) well, then SVMs will win out. But for the majority of the settings, they're either the same or logreg is a bit better.

As a result, what do I do? I use logreg with lambda=1. That's it. No tuning, no nothing.

(Note that, as I said before, I haven't ever run experiments to verify this. I think it would be a moderately interesting thing to try to see if it really holds up when all else -- eg., the optimization algorithm, early stopping, implementation, choice of regularizer (L1, L2, KL, etc.), and so on -- are held constant... maybe it's not true. But if it is, then it's an interesting theoretical question: hinge loss and log loss don't look that different, despite the fact that John seems to not like how log loss diverges: why should this be true?)

This is also why I use averaged perceptron: there aren't any hyperparameters to select. It just runs.

What I'd really like to see in future "yet another classifier" papers is an analysis of sensitivity to hyperparameter selection. You could provide graphs and stuff, but these get hard to read. I like numbers. I'd like a single number that I can look at. Here are two concrete proposals for what such a number could be (note: I'm assuming you're also going to provide performance numbers at the best possible selection of hyperparameters from development data or cross validation... I'm talking about something in addition):

1. Performance at a default setting of the hyperparameter. For instance, SVM-light uses something like average inverse norm of the data vectors as the C parameter. Or you could just us 1, like I do for logreg. In particular, suppose you're testing your algorithm on 20 data sets from UCI. Pick a single regularization parameter (or parameter selection scheme, ala SVM-light) to use for all of them and report results using that value. If this is about the same as the "I carefully tuned" setting, I'm happy. If it's way worse, I'm not so happy.
2. Performance within a range. Let's say that if I do careful hyperparameter selection then I get an accuracy of X. How large is the range of hyperparameters for which my accuracy is at least X*0.95? I.e., if I'm willing to suffer 5% multiplicative loss, how lazy can I be about hp selection? For this, you'll probably need to grid out your performance and then do empirical integration to approximate this. Of course, you'll need to choose a bounded range for your hp (usually zero will be a lower bound, but you'll have to pick an upper bound, too -- but this is fine: as a practitioner, if you don't give me an upper bound, I'm going to be somewhat unhappy).
   

Neither of these is totally ideal, but I think they'd be a lot better than the current situation of really having no idea! Maybe there are other proposals out there that I don't know about, or maybe other readers have good ideas. But for me, if you're going to convince me to switch to your algorithm, this is something that I really really want to know.

(As an aside, Mark, if you're reading this, I can imagine the whole CW thing getting a bit confused if you're using feature hashing: have you tried this? Or has someone else?)

ACS: Machine Translation Papers at EMNLP

[Guest Post by Adam Lopez... thanks, Adam! Hal's comment: you may remember that a while ago I proposed the idea of conference area chairs posting summaries of their areas; well, Adam is the first to take me up on this idea... I still think it's a good idea, so anyone else who wants to do so in the future, let me know!]

Conferences can be exhausting, and back-to-back conferences can be really exhausting, so I want to convince you to pace yourself and save some energy for EMNLP at the end of the week, because we have some really interesting MT papers. I'll focus mainly on oral presentations, because unlike poster sessions, the parallel format of the oral sessions entails a hard choice between mutually exclusive options, and part of my motivation is to help you make that choice. That being said, there are many interesting papers at the poster session, so do take a look at them!

MT is a busy research area, and we have a really diverse set of papers covering the whole spectrum of ideas: from blue sky research on novel models, formalisms, and algorithms, to the hard engineering problems of wringing higher accuracy and speed out of a mature, top-scoring NIST system. I occasionally feel that my colleagues on far reaches of either side of this spectrum are too dismissive of work on the other side; we need both if we're going to improve translation.

Outside the Box

Before giving you a guided tour through that spectrum, I want to highlight one paper that I found thought-provoking, but hard to classify. Zaidan & Callison-Burch question a basic assumption underlying most machine learning approaches to NLP: that we must optimize on an easily computable approximation to the true loss function. They ask: why not optimize for human judgement? They design a metric that uses judgements on small snippets of a target sentence (defined by a spanning nonterminal in a parse tree of the aligned source sentence) and figure how many judgements they would need to collect (using Amazon Mechanical Turk) to cover an iteration of MERT, exploiting the fact that these snippets reoccur repeatedly during optimization. How hard is this exactly? I would say, in terms of this scale of loss functions, that their metric is a 2. Yet, it turns out to be cheap and fast to compute. The paper doesn't report results of an actual optimization run, but it's in the works... hopefully you'll learn more at the conference.

Connecting Theory and Practice

A few papers combine deep theoretical insight with convincing empirical results. Hopkins & Langmead improve on cube pruning, a popular approximate search technique for structured models with non-local features (i.e. translation with an integrated language model). They move cube pruning from its ad hoc roots to a firm theoretical basis by constructing a reduction to A* search, connecting it to classical AI search literature. This informs the derivation of new heuristics for a syntax-based translation model, including an admissible heuristic to perform exact cube pruning. It's still globally approximate, but exact for the local prediction problem that cube pruning solves (i.e., what are the n-best state splits of an item, given the n-best input states from previous deductions?). Amazingly, this is only slightly slower than the inexact version and improves the accuracy of a strong baseline on a large-scale Arabic-English task.

Li & Eisner show how to compute a huge number of statistics efficiently over a combinatorially large number of hypotheses represented in a hypergraph. The statistics include expected hypothesis length, feature expectation, entropy, cross-entropy, KL divergence, Bayes risk, variance of hypothesis length, gradient of entropy and Bayes risk, covariance and Hessian matrix. It's beautifully simple: they recast the quantities of interest as semirings and run the inside (or inside-outside) algorithm. As an example application, they perform minimum risk training on a small Chinese-English task, reporting gains in accuracy. For a related paper on minimum risk techniques, see the poster by Pauls et al.

Novel Modeling and Learning Approaches

Tromble & Eisner also connect translation to theory by way of a novel model, framing reordering as an instance of the linear ordering problem: given a matrix of pairwise ordering preferences between all words in a sentence, can we find a permutation that optimizes the global score? This is NP-hard, but they give a reasonable approximation based on ITG, with some clever dynamic programming tricks to make it work. Then they show how to learn the matrix and use it to reorder test sentences prior to translation, improving over the lexicalized reordering model of Moses on German-English.

However, most of the new models at EMNLP are syntax-based. In the last few years, syntax-based modeling has focused primarily on variants of synchronous context-free grammar (SCFG). This year there's a lot of work investigating more expressive formalisms.

Two papers model translation with restricted variants of synchronous tree-adjoining grammar (STAG). Carreras & Collins model syntax atop phrase pairs with a parser using sister adjunction (as in their 2008 parser). The model resembles a synchronous version of Markov grammar, which also connects it to recent dependency models of translation (e.g. Shen et al. 2008, Galley et al. 2009, Gimpel & Smith below, and Hassan et al. in the poster session). Decoding is NP-complete, and devising efficient beam search is a key point in the paper. The resulting system outperforms Pharaoh on German-English. DeNeefe & Knight model target-side syntax via synchronous tree insertion grammar (STIG). It's similar to synchronous tree substitution grammar (STSG; previously realized in MT as GHKM) with added left- and right-adjunction operations to model optional arguments. They show how to reuse a lot of the STSG machinery via a grammar transformation from STIG to STSG, and the results improve on a strong Arabic-English baseline.

Gimpel & Smith use a relatively new formalism: quasi-synchronous dependency grammar (QDG). In quasi-synchronous grammar, the generation of a target syntax tree is conditioned on (but not necessarily isomorphic to) a source syntax tree. Formally, each target node can be annotated with any source node. Since in dependency grammar the nodes are words, their QDG model resembles a word-to-word model. Decoding with QDG was not obvious given past work, and is one of several novel contributions of the paper. Another is the idea that all possible biphrases can fire an associated feature, regardless of overlap. Kääriäinen makes this idea central. Instead of reasoning over the latent derivations of a generative model, his model directly optimizes a feature-based representation of the target sentence, where the features consist of any biphrase in the training set (per standard heuristics). This raises some new problems -- such as how to find the target sentence given the optimal feature vector -- which are solved with dynamic programming. The decoder doesn't quite beat Moses when used with a language model, but it's an order of magnitude faster!

Three other papers operate on STSG models, with an emphasis on learning techniques. Cohn & Blunsom reformulate tree-to-string STSG induction as a problem in non-parametric Bayesian inference, extending their TSG model for monolingual parsing, and removing the dependence on heuristics over noisy GIZA++ word alignments. The model produces more compact rules, and outperforms GHKM on a Chinese-English task. This is a hot topic: check out Liu & Gildea's poster for an alternative Bayesian formulation of the same problem and language pair. Galron et al. look at tree-to-tree STSG (from a Data-Oriented Parsing perspective), with an eye towards discriminatively learning STSG rules to optimize for translation accuracy.

Bayesian inference also figures in the model of Chung & Gildea, who aim at bilingually-informed segmentation of a source language. The model is like IBM Model 1, except that the source positions are actually substrings of the source instead of single positions. Reasoning over the substring boundaries makes it resemble an HMM, and they use a sparse prior to avoid overfitting. Tokenizing new text uses the marginal distribution on source language segmentations, and this performs almost as well as a supervised segmenter on Chinese, and better on Korean, in end-to-end translation.

SCFG models aren't completely forgotten: Zhang & Li offer a new twist on reordering in binary-branching SCFG. Given a source parse, we could train a maximum entropy classifier to decide whether any binary production should be inverted; this requires a lot of computation over sparse vectors. They instead represent the features implicitly using a tree convolution kernel, showing nice gains in Chinese-English.

On the algorithmic side, Levenberg & Osborne look at language modeling under the condition that we have unbounded data streams in both source and target language, bounded computation, and the desire to bias our language model towards more recent language use without constantly retraining it. They accomplish this with online perfect hashing (extending previous work) in a succinct data structure that supports deletions, showing that they can draw on recent information in both the source and the target to incrementally update the model while keeping a bounded memory footprint.

Bai et al. focus on the problem of acquiring multiword expressions (i.e. idioms), showing why typical word alignment methods fail, and using a combination of statistical association measures and heuristics to fix the problem, with small gains in Chinese-English.

Decoding

Since SCFG models have become mainstream, there's been a greater emphasis on decoding. Following a recent strand of research on grammar transformations for SCFG, Xiao et al. observe that, in the space of possible transformations, many will pair source yields with huge numbers of target yields, which compete during decoding and thus result in more search errors. The trick is to select a transform that distributes target yields more evenly across source yields. They pose this as an optimization problem and give a greedy algorithm; the resulting grammar is reliably better under a variety of conditions on a Chinese-English task. Meanwhile, Zhang et al. engineer more efficient STSG decoding for the case in which the source is a parse forest and source units are tree fragments. The trick is to encode translation rules in the tree path equivalent of a prefix tree. On Chinese-English this improves decoding speed and ultimately translation accuracy, because the decoder can consider larger fragments much more efficiently. Finally, see Finch & Sumita's comprehensive poster on bidirectional phrase-based decoding for a huge number of language pairs.

Onwards and Upwards

The align/extract/MERT pipeline popularized by Moses and other NIST-style systems is incredibly hard to improve, but several papers manage just that.

Hermjakob's word aligner starts from lexical translation parameters learned by a statistical alignment model. Then, following some fairly general observations on different linguistic classes of words, it uses some well-motivated heuristics to fix a whole bunch of little things that many more principled models ignore: the different behavior of content words (improved via careful manipulation of pointwise mutual information) and function words (improved via constraints from parse structure) is treated along with careful handling of numbers, transliterations, and morphology to give strong improvements in Arabic-English.

Liu et al. then extract phrases by relaxing standard heuristic constraints. Given a posterior probability for every alignment point, they simply calculate the probability that a phrase would be extracted, and use this as their count in the typical frequency-based estimate. It's efficient and improves Chinese-English.

Three papers incorporate new feature types into strong baseline translation models, following a recent trend. Shen et al. devise some clever local features using source-side context, derivation span length, and dependency modeling to make impressive improvements on an already impressive baseline system in both Chinese-English and Arabic-English. Matsoukas et al. then show how a mixed-genre system can effectively be adapted for a particular target domain, by using a small amount data to tune weights tied to genre and collection types in the training corpus, again with strong results in Arabic-English. Mauser et al. take their previous triplet lexicon model (a probabilistic feature using an outside source word as additional conditioning context) and move it from a reranking step into the decoding step, with a nice experimental treatment showing improvements in large-scale Chinese-English and Arabic-English.

If you've seen the latest NIST results, you know that system combination gives huge improvements. Check out posters by He & Toutanova, Duan et al., and Feng et al. to learn the latest techniques. Last but not least, if you need a strategy for language pairs with very little parallel data, the poster by Nakov & Ng will interest you.

Thanks

EMNLP was the first time I've been area chair for a conference, and it was really rewarding to work with such great volunteers and< to see the great papers that were selected (I should note here that I included two papers not on my track that I'm quite familiar with -- the ones from Edinburgh). It was also very enlightening, but that's another story. Many thanks to Hal for offering this forum to share the results!

Destination: Singapore

Welcome to everyone to ACL! It's pretty rare for me to end up conferencing in a country I've been before, largely because I try to avoid it. When I was here last time, I stayed with Yee Whye, who was here at the time as a postdoc at NUS, and lived here previously in his youth. As a result, he was an excellent "tour guide." With his help, here's a list of mostly food related stuff that you should definitely try while here (see also the ACL blog):

• Pepper crab. The easiest to find are the "No Signboard" restaurant chain. Don't wear a nice shirt unless you plan on doing laundry.
  
• Chicken rice. This sounds lame. Sure, chicken is kind of tasty. Rice is kind of tasty. But the key is that the rice is cooked in or with melted chicken fat. It's probably the most amazingly simple and delicious dish I've ever had. "Yet Kun" (or something like that) is along Purvis street.
• Especially for dessert, there's Ah Chew, a Chinese place around Liang Seah street in the Bugis area (lots of other stuff there too).
• Hotpot is another local specialty: there is very good spicy Szechuan hotpot around Liang Seah street.
• For real Chinese tea, here. (Funny aside: when I did this, they first asked "have you had tea before?" Clearly the meaning is "have you had real Chinese tea prepared traditionally and tasted akin to a wine tasting?" But I don't think I would ever ask someone "have you had wine before?" But I also can't really think of a better way to ask this!)
• Good late night snacks can be found at Prata stalls (eg., indian roti with curry).
• The food court at Vivocity, despite being a food court, is very good. You should have some hand-pressed sugar cane juice -- very sweet, but very tasty (goes well with some spicy hotpot).
• Chinatown has good Chinese dessert (eg., bean stuff) and frog leg porridge.

Okay, so this list is all food. But frankly, what else are you going to do here? Go to malls? :). There's definitely nice architecture to be seen; I would recommend the Mosque off of Arab street; of course you have to go to the Esplanade (the durian-looking building); etc. You can see a few photos from my last trip here.

Now, I realize that most of the above list is not particularly friendly to my happy cow friends. Here's a list of restaurants that happy cow provides. There are quite a few vegetarian options, probably partially because of the large Muslim population here. There aren't as many vegan places, but certainly enough. For the vegan minded, there is a good blog about being vegan in Singapore (first post is about a recent local talk by Campbell, the author of The China Study, which I recommend everyone at least reads). I can't vouch for the quality of these places, but here's a short list drawn from Living Vegan:

• Mushroom hotpot at Ling Zhi
• Fried fake meat udon noodles (though frankly I'm not a big fan of fake meat)
• Green Pasture cafe; looks like you probably have to be a bit careful here in terms of what you order
• Yes Natural; seems like it has a bunch of good options
• Lotus Veg restaurant, seems to have a bunch of dim sum (see here, too)
  
• If you must, there's pizza
• And oh-my-gosh, there's actually veggie chicken rice, though it doesn't seem like it holds up to the same standards as real chicken rice (if it did, that would be impressive)

Okay, you can find more for yourself if you go through their links :).

Enjoy your time here!

Quick update: Totally forgot about coffee. If you need your espresso kick, Highlander coffee (49 Kampong Bahru Road) comes the most recommended, but is a bit of a hike from the conference area. Of course, you could also try the local specialty: burnt crap with condensed milk (lots and lots of discussion especially on page two here).

Non-parametric as memorizing, in exactly the wrong way?

There is a cool view of the whole non-parametric Bayes thing that I think is very instructive. It's easiest to see in the case of the Pitman-Yor language modeling work by Frank Wood and Yee Whye Teh. The view is "memorize what you can, and back off (to a parametric model) when you can't." This is basically the "backoff" view... where NP Bayes comes in is to control the whole "what you can" aspect. In other words, if you're doing language modeling, try to memorize two grams; but if you haven't seen enough to be confident in your memorization, back off to one grams; and if you're not confident there, back off to a uniform distribution (which is our parametric model -- the base distribution).

Or, if you think about the state-splitting PCFG work (done both at Berkeley and at Stanford), basically what's going on is that we're memorizing as many differences of tree labels as we can, and then backing off to the "generic" label when memorization fails. Or if we look at Trevor Cohn's NP-Bayes answer to DOP, we see a similar thing: memorize big tree chunks, but if you can't, fall back to a simple CFG (our parametric model).

Now, the weird thing is that this mode of memorization is kind of backwards from how I (as an outsider) typically interpret cognitive models (any cogsci people out there, feel free to correct me!). If you take, for instance, morphology, there's evidence that this is exactly not what humans do. We (at least from a popular science) perspective, basically memorize simple rules and then remember exceptions. That is, we remember that to make the past tense of a verb, we add "-ed" (the sound, not the characters) but for certain verbs, we don't: go/went, do/did, etc. You do little studies where you ask people to inflect fake words and they generally follow the rule, not the exceptions (but see * below).

If NP Bayes had its way on this problem (or at least if the standard models I'm familiar with had their way), they would memorize "talk" -> "talked" and "look" -> "looked" and so on because they're so familiar. Sure, it would still memorize the exceptions, but it would also memorize the really common "rule cases too... why? Because of course it could fall back to the parametric model, but these are so common that the standard models would really like to take advantage of the rich-get-richer phenomenon on things like DPs, thus saving themselves cost by memorizing a new "cluster" for each common word. (Okay, this is just my gut feeling about what such models would do, but I think it's at least defensible.) Yes, you could turn the DP "alpha" parameter down, but I guess I'm just not convinced this would do the right thing. Maybe I should just implement such a beast but, well, this is a blog post, not a *ACL paper :P.

Take as an alternative example the language modeling stuff. Basically what it says is "if you have enough data to substantiate memorizing a 5 gram, you should probably memorize a 5 gram." But why? If you could get the same effect with a 2 or 3 gram, why waste the storage/time?!

I guess you could argue "your prior is wrong," which is probably true for most of these models. In which case I guess the question is "what prior does what I want?" I don't have a problem with rich get richer -- in fact, I think it's good in this case. I also don't have a problem with a logarithmic growth rate in the number of exceptions (though I'd be curious how this holds up empirically -- in general, I'm a big fan of checking if your prior makes sense; for instance, Figure 3 (p16) of my supervised clustering paper). I just don't like the notion of memorizing when you don't have to.

(*) I remember back in grad school a linguist from Yale came and gave a talk at USC. Sadly, I can't remember who it was: if anyone wants to help me out, I'd really appreciate it! The basic claim of the talk is that humans actually memorize a lot more than we give them credit for. The argument was in favor of humans basically memorizing all morphology and not backing off to rules like "add -ed." One piece of evidence in favor of this was timing information for asking people to inflect words: the timing seemed to indicate a linear search through a long list of words that could possibly be inflected. I won't say much more about this because I'm probably already misrepresenting it, but it's an interesting idea. And, if true, maybe the NP models are doing exactly what they should be doing!

Small changes beget good or bad examples?

If you compare vision research with NLP research, there are a lot of interesting parallels. Like we both like linear models. And conditional random fields. And our problems are a lot harder than binary classification. And there are standard data sets that we've been evaluating on for decades and continue to evaluate on (I'm channeling Bob here :P).

But there's one thing that happens, the difference of which is so striking, that I'd like to call it to center stage. It has to do with "messing with our inputs."

I'll spend a bit more time describing the vision approach, since it's probably less familiar to the average reader. Suppose I'm trying to handwriting recognition to identify digits from zero to nine (aka MNIST). I get, say, 100 labeled zeros, 100 labeled ones, 100 labeled twos and so on. So a total of 1000 data points. I can train any off the shelf classifier based on pixel level features and get some reasonable performance (maybe 80s-90s, depending).

Now, I want to insert knowledge. The knowledge that I want to insert is some notion of invariance. I.e., if I take an image of a zero and translate it left a little bit, it's still a zero. Or up a little bit. Of if I scale it up 10%, it's still a zero. Or down 10%. Or if I rotate it five degrees. Or negative five. All zeros. Same hold for all the other digits.

One way to insert this knowledge is to muck with the learning algorithm. That's too complicated for me: I want something simpler. So what I'll do is take my 100 zeros and 100 ones and so on and just manipulate them a bit. That is, I'll sample a random zero, and apply some small random transformations to it, and call it another labeled example, also a zero. Now I have 100,000 training points. I train my off the shelf classifier based on pixel level features and get 99% accuracy or more. The same trick works for other vision problem (eg., recognizing animals). (This process is so common that it's actually described in Chris Bishop's new-ish PRML book!)

This is what I mean by small changes (to the input) begetting good example. A slightly transformed zero is still a zero.

Of course, you have to be careful. If you rotate a six by 180 degrees, you get a nine. If you rotate a cat by 180 degrees, you get an unhappy cat. More seriously, if you're brave, you might start looking at a class of transformations called diffeomorphisms, which are fairly popular around here. These are nice because of their nice mathematical properties, but un-nice because they can be slightly too flexible for certain problems.

Now, let's go over to NLP land. Do we ever futz with our inputs?

Sure!

In language modeling, we'll sometimes permute words or replace one word with another to get a negative example. Noah Smith futzed with his inputs in contrastive estimation to produce negative examples by swapping adjacent words, or deleting words.

In fact, try as I might, I cannot think of a single case in NLP where we make small changes to an input to get another good input: we always do it to get a bad input!

In a sense, this means that one thing that vision people have that we don't have is a notion of semantics preserving transformations. Sure, linguists (especially those from that C-guy) study transformations. And there's a vague sense that work in paraphrasing leads to transformations that maintain semantic equivalence. But the thing is that we really don't know any transformations that preserve semantics. Moreover, some transformations that seem benign (eg., passivization) actually are not: one of my favorite papers at NAACL this year by Greene and Resnik showed that syntactic structure affects sentiment (well, them, drawing on a lot of psycholinguistics work)!

I don't have a significant point to this story other than it's kind of weird. I mentioned this to some people at ICML and got a reaction that replacing words with synonyms should be fine. I remember doing this in high school, when word processors first started coming with thesauri packed in. The result seemed to be that if I actually knew the word I was plugging in, life was fine... but if not, it was usually a bad replacement. So this seems like something of a mixed bag: depending on how liberal you are with defining "synonym" you might be okay do this, but you might also not be.

ICML/COLT/UAI 2009 retrospective

This will probably be a bit briefer than my corresponding NAACL post because even by day two of ICML, I was a bit burnt out; I was also constantly swapping in other tasks (grants, etc.). Note that John has already posted his list of papers.

1. #317: Multi-View Clustering via Canonical Correlation Analysis (Chaudhuri, Kakade, Livescu, Sridharan). This paper shows a new application of CCA to clustering across multiple views. They use some wikipedia data in experiments and actually prove something about the fact that (under certain multi-view-like assumptions), CCA does the "right thing."
   
2. #295: Learning Nonlinear Dynamic Models (Langford, Salakhutdinov,, Zhang). The cool idea here is to cut a deterministic classifier in half and use its internal state as a sort of sufficient statistic. Think about what happens if you represent your classifier as a circuit (DAG); then anywhere you cut along the circuit gives you a sufficient representation to predict. To avoid making circuits, they use neural nets, which have an obvious "place to cut" -- namely, the internal nodes.
3. #364: Online Dictionary Learning for Sparse Coding (Mairal, Bach, Ponce, Sapiro). A new approach to sparse coding; the big take-away is that it's online and fast.
4. 394: MedLDA: Maximum Margin Supervised Topic Models for Regression and Classification (Zhu, Ahmed, Xing). This is a very cute idea for combining objectives across topic models (namely, the variational objective) and classification (the SVM objective) to learn topics that are good for performing a classification task.
5. #393: Learning from Measurements in Exponential Families (Liang, Jordan, Klein). Suppose instead of seeing (x,y) pairs, you just see some statistics on (x,y) pairs -- well, you can still learn. (In a sense, this formalizes some work out of the UMass group; see also the Bellare, Druck and McCallum paper at UAI this year.)
6. #119: Curriculum Learning (Bengio, Louradour, Collobert, Weston). The idea is to present examples in a well thought-out order rather than randomly. It's a cool idea; I've tried it in the context of unsupervised parsing (the unsearn paper at ICML) and it never helped and often hurt (sadly). I curriculum-ified by sentence length, though, which is maybe not a good model, especially when working with WSJ10 -- maybe using vocabulary would help.
7. #319: A Stochastic Memoizer for Sequence Data (Wood, Archambeau, Gasthaus, James, Whye Teh). If you do anything with Markov models, you should read this paper. The take away is: how can I learn a Markov model with (potentially) infinite memory in a linear amount of time and space, and with good "backoff" properties. Plus, there's some cool new technology in there.
8. A Uniqueness Theorem for Clustering Reza Bosagh Zadeh, Shai Ben-David. I already talked about this issue a bit, but the idea here is that if you fix k, then the clustering axioms become satisfiable, and are satisfied by two well known algorithms. Fixing k is a bit unsatisfactory, but I think this is a good step in the right direction.
9. Convex Coding David Bradley, J. Andrew Bagnell. The idea is to make coding convex by making it infinite! And then do something like boosting.
10. On Smoothing and Inference for Topic Models Arthur Asuncion, Max Welling, Padhraic Smyth, Yee Whye Teh. If you do topic models, read this paper: basically, none of the different inference algorithms do any better than the others (perplexity-wise) if you estimate hyperparameters well. Come are, of course, faster though.
11. Correlated Non-Parametric Latent Feature Models Finale Doshi-Velez, Zoubin Ghahramani. This is an indian-buffet-process-like model that allows factors to be correlated. It's somewhat in line with our own paper from NIPS last year. There's still something a bit unsatisfactory in both our approach and their approach that we can't do this "directly."
12. Domain Adaptation: Learning Bounds and Algorithms. Yishay Mansour, Mehryar Mohri and Afshin Rostamizadeh. Very good work on some learning theory for domain adaptation based on the idea of stability.

Okay, that's it. Well, not really: there's lots more good stuff, but those were the things that caught my eye. Feel free to tout your own favorites in the comments.

Should there be a shared task for semi-supervised learning in NLP?

(Guest post by Kevin Duh. Thanks, Kevin!)

At the NAACL SSL-NLP Workshop recently, we discussed whether there ought to be a "shared task" for semi-supervised learning in NLP. The panel discussion consisted of Hal Daume, David McClosky, and Andrew Goldberg as panelists and audience input from Jason Eisner, Tom Mitchell, and many others. Here we will briefly summarize the points raised and hopefully solicit some feedback from blog readers.

Three motivations for a shared task

A1. Fair comparison of methods: A common dataset will allow us to compare different methods in an insightful way. Currently, different research papers use different datasets or data-splits, making it difficult to draw general intuitions from the combined body of research.

A2. Establish a methodology for evaluating SSLNLP results: How exactly should a semi-supervised learning method be evaluated? Should we would evaluate the same method for both low-resource scenarios (few labeled points, many unlabeled points) and high-resource scenarios (many labeled points, even more unlabeled points)? Should we evaluate the same method under different ratios of labeled/unlabeled data? Currently there is no standard methodology for evaluating SSLNLP results, which means that the completeness/quality of experimental sections in research papers varies considerably.

A3. Encourage more research in the area: A shared task can potentially lower the barrier of entry to SSLNLP, especially if it involves pre-processed data and community support network. This will make it easier for researchers in outside fields, or researchers with smaller budgets to contribute their expertise to the field. Furthermore, a shared task can potentially direct the community research efforts in a particular subfield. For example, "online/lifelong learning for SSL" and "SSL as joint inference of multiple tasks and heterogeneous labels" (a la Jason Eisner's keynote) were identified as new, promising areas to focus on in the panel discussion. A shared task along those lines may help us rally the community behind these efforts.

Arguments against the above points

B1. Fair comparison: Nobody really argues against fair comparison of methods. The bigger question, however, is whether there exist a *common* dataset or task where everyone is interested in. At the SSLNLP Workshop, for example, we had papers in a wide range of areas ranging from information extraction to parsing to text classification to speech. We also had papers where the need for unlabeled data is intimately tied in to particular components of a larger system. So, a common dataset is good, but what dataset can we all agree upon?

B2. Evaluation methodology: A consistent standard for evaluating SSLNLP results is nice to have, but this can be done independently from a shared task through, e.g. an influential paper or gradual recognition of its importance by reviewers. Further, one may argue: what makes you think that your particular evaluation methodology is the best? What makes you think people will adopt it generally, both inside and outside of the shared task?

B3. Encourage more research: It is nice to lower the barriers to entry, especially if we have pre-processed data and scripts. However, it has been observed in other shared tasks that often it is the pre-processing and features that matter most (more than the actual training algorithm). This presents a dilemma: If the shared task pre-processes the data to make it easy for anyone to join, will we lose the insights that may be gained via domain knowledge? On the other hand, if we present the data in raw form, will this actually encourage outside researchers to join the field?

Rejoinder

A straw poll at the panel discussion showed that people are generally in favor of looking into the idea of a shared task. The important question is how to make it work, and especially how to address counterpoints B1 (what task to choose) and B3 (how to prepare the data). We did not have enough time during the panel discussion to go through the details, but here are some suggestions:

• We can view NLP problems as several big "classes" of problems: sequence prediction, tree prediction, multi-class classification, etc. In choosing a task, we can pick a representative task in each class, such as name-entity recognition for sequence prediction, dependency parsing for tree prediction, etc. This common dataset won't attract everyone in NLP, but at least it will be relevant for a large subset of researchers.
  
  
• If participants are allowed to pre-process their own data, the evaluation might require participant to submit a supervised system along with their semi-supervised system, using the same feature set and setup, if possible. This may make it easier to learn from results if there are differences in pre-processing.
  
  
• There should also be a standard supervised and semi-supervised baseline (software) provided by the shared task organizer. This may lower the barrier of entry for new participants, as well as establish a common baseline result.
  

Any suggestions? Thoughts?

Why I Don't Buy Clustering Axioms

In NIPS 15, Jon Kleinberg presented some impossibility results for clustering. The idea is to specify three axioms that all clustering functions should obey and examine those axioms.

Let (X,d) be a metric space (so X is a discrete set of points and d is a metric over the points of X). A clustering function F takes d as input and produces a clustering of the data. The three axioms Jon states that all clustering functions should satisfy are:

1. Scale invariance: For all d, for all a>0, F(ad) = F(d). In other words, if I transform all my distances by scaling them uniformly, then the output of my clustering function should stay the same.
2. Richness: The range of F is the set of all partitions. In other words, there isn't any bias that prohibits us from producing some particular partition.
3. Consistency: Suppose F(d) gives some clustering, C. Now, modify d by shrinking distances within clusters of C and expanding distances between clusters in C. Call the new metric d'. Then F(d') = C.

Kleinberg's result is that there is no function F that simultaneously satisfies all these requirements. Functions can satisfy two, but never all three. There have been a bunch of follow on papers, including one at NIPS last year and one that I just saw at UAI.

If you think about these axioms a little bit, they kind of make sense. My problem is that if you think about them a lot of bit, you (or at least I) realize that they're broken. The biggest broken one is consistency, which becomes even more broken when combined with scale invariance.

What I'm going to do to convince you that consistency is broken is start with some data in which there is (what I consider) a natural clustering into two clusters. I'll then apply consistency a few times to get something that (I think) should yield a different clustering.

Let's start with some data. The colors are my opinion as to how the data should be clustered:

I hope you agree with my color coding. Now, let's apply consistency. In particular, let's move some of the red points, only reducing inter-clustering distances. Formally, we find the closest pair of points and move things toward those.

The arrows denote the directions these points will be moved. To make the situation more visually appealing, let's move things into lines: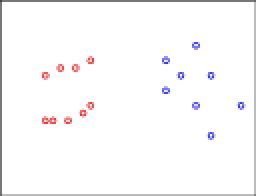
Okay, this is already looking funky. Let's make it even worse. Let's apply consistency again and start moving some blue points:
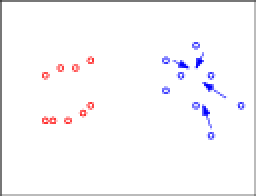Again, let's organize these into a line:
And if I had given you this data to start with, my guess is the clustering you'd have come up with is more like:
This is a violation of consistency.

So, what I'd like someone to do is to argue to my why consistency is actually a desirable property.

I can come up with lots of other examples. One reason why this invariance is bad is because it renders the notion of "reference sizes" irrelevant. This is of course a problem if you have prior knowledge (eg., one thing measured in millimeters, the other in kilometers). But even in the case where you don't know knowledge, what you can do is take the following. Take data generated by thousands of well separated Gaussians, so that the clearly right thing to do is have one cluster per Gaussian. Now, for each of these clusters except for one, shrink them down to single points. This is possible by consistency. Now, your data basically looks like thousands-1 of clusters with zero inter-cluster distances and then one cluster that's spread out. But now it seems that the reasonable thing is to put each data point that was in this old cluster into its own cluster, essentially because I feel like the other data shows you what clusters should look like. If you're not happy with this, apply scaling and push these points out super far from each other. (I don't think this example is as compelling as the one I drew in pictures, but I still think it's reasonable.

Now, in the UAI paper this year, they show that if you fix the number of clusters, these axioms are now consistent. (Perhaps this has to do with the fact that all of my "weird" examples change the number of clusters -- though frankly I don't think this is necessary... I probably could have arranged it so that the resulting green and blue clusters look like a single line that maybe should just be one cluster by itself.) But I still feel like consistency isn't even something we want.

(Thanks to the algorithms group at Utah for discussions related to some of these issues.)

UPDATE 20 JUNE 2009, 3:49PM EST

Here's some data to justify the "bad things happen even when the number of clusters stays the same" claim.

Start with this data:


Now, move some points toward the middle (note they have to spread to the side a bit so as not to decrease intra-cluster distances).

Yielding data like the following:

Now, I feel like two horizontal clusters are most natural here. But you may disagree. What if I add some more data (ie., this is data that would have been in the original data set too, where it clearly would have been a third cluster):

And if you still disagree, well then I guess that's fine. But what if there were hundreds of other clusters like that.

I guess the thing that bugs me is that I seem to like clusters that have similar structures. Even if some of these bars were rotated arbitrarily (or, preferably, in an axis-aligned manner), I would still feel like there's some information getting shared across the clusters.